Olimpiade Sains Provinsi (OSP) 2017 - Komputer
Berapakah digit kedua dari belakang dari nilai 111^112^113?
Pak Dengklek sangat suka mengutak-atik bilangan dan memberikan nama untuk sifat unik dari sebuah bilangan. Salah satu sifat unik bilangan yang dlsukal oleh Pak Dengklek adalah Bilangan Menanjak. Sebuah bilangan X disebut Bilangan Menanjak apabila digit-digit dari X menaik dari kiri ke kanan. Conteh Bilangan
Menanjak adalah 122349. Tiba-tiba Pak Dengklek penasaran, ada berapa Bilangan Menanjak yang nilainya yang kurang dari (10^10)?
Bilangan unik lainnya yang disukai Pak Dengklek adalah Bilangan Kompeten. Sebuah bilangan X disebut Bilangan Kompeten apabila digit-digit dart X menurun atau menaik dari kiri ke kanan. Contoh Bilangan Kompeten yang menaik adalah 12234 dan contoh Bilangan Kompeten yang menurun adalah 9844200. Tiba-tiba Pak Dengklek penasaran, ada berapa Bilangan Kompeten yang nilainya kurang dari (10^10)?
Pak Dengklek baru saja membeli 100 alien untuk peternakannya. Harga alien ditentukan oleh kakinya. Pak Dengklek membayar masing-masing 15 Zru untuk alien yang berkaki 2, masing-masing 40 Zru untuk alien yang berkaki 4, dan masing-masing 70 Zru untuk alien yang berkaki 6. Beberapa hari setelah membelinya, Pak Dengklek sadar bahwa ternyata ia alergi terhadap alien-alien tersebut. Pak Dengklek ingin segera menjual seluruh alien yang telah dibelinya, tetapi ketika bertemu dengan seorang pembeli dia lupa berapa jumlah masing-masing jenis alien, yang dia ingat hanyalah kaki mereka yang berjumlah 374. Berapa Zru minimal yang harus ditawarkan Pak Dengklek agar dia tidak akan rugi?
Deskripsi untuk soal nomor 5 - 7
Diberikan deret dari n buah bilangan bulat positif berbeda terurut menaik dari kiri ke kanan, al, a2, .... Terhadap deret itu akan dilakukan langkah-langkah berikut:
(1). Berikan tanda negatif/positif pada deret tersebut sehingga didapat salah satu kemungkinan deret baru B:
a. +al, -a2, +a3, .... , atau
b. -al, +a2, -a3, ..
(2). lnisialisasi Sum= 0.
(3). Ambil sembarang bilangan X dari B.
(4). Tambahkan X pada Sum. Apabila Sum berharga positif tuliskan huruf P, atau apabila negatif tuliskan N, dan apabila nol tuliskan 0.
(5). Jika B tidak kosong, tentukan Y yang semula berada tepat di sebelah (kiri atau kanan) X untuk menggantikan X. Jika B kosong, hentikan proses, dan anda mendapatkan hasil deretan huruf {P, N, O} dengan urutan sesuai dengan yang diperoleh di langkah (4).
(6). Kembali ke aturan (4).
Diberikan S bilangan: 2 7 10 13 21, tentukan bilangan pertama yang harus diambil apabila pola tulisan yang ingin didapat adalah PPNPN (tulis -1 jika tidak mungkin).
Diberikan 7 bilangan: 1 4 5 7 8 10 17, tentukan bilangan pertama yang harus diambll apabita pola tulisan yang ingin didapat adalah PONNPNN (tulis -1 jika tidak mungkin).
Apabila bilangan yang diberikan adalah K~{l,2,3, .. ,1000), tentukan bilangan pertama yang harus diambil apabila pola tulisan yang ingin didapat adalah PPNNPPNN ••• PPNNPPNN.
Pak Dengklek memiliki suatu kandang dengan x sapi di dalamnya (x ditentukan kemudian). Pada hari ke-n, ada m sapi yang akan dijual. Pak Dengklek akan mengambil sapi sejumlah suatu bilangan prima yang menaik setiap hari, sehingga pada hari ke satu mengambll 2 sapi, hari kedua mengambil 3 sapi, hari ketiga mengambil 5 sapi, dan seterusnya. Pak Dengklek kecewa saat ia ingin mengambil sejumlah sapi yang diharapkannya untuk dijual namun sapinya tak cukup lagi atau habis. Sekarang, terdapat 500 sapi. Pada hari keberapakah Pak Dengklek kecewa karena tak dapat mengambil sapi sejumlah sapi yang diharapkan dapat dijualnya?
Diberikan petak 2 dimensi sebagai berikut dengan keterangan: . -> jalur yang dapat dilalui # -> jalur yang tidak dapat dilalui X -> titik mulai Y -> titik selesai ########### #.##..#...# #....#..#.# #...##...## #.#...Y#..# #.#...#.#.# #.##.#....# #X.....##.# ###########
Sebuah robot bergerak dengan algoritma sebagai berikut:
- Selama dapat bergerak ke atas dan belum dikunjungi, ke atas
- Kalau tak dapat ke atas atau sudah dikunjungi, ke kanan
- Kalau tak dapat ke kanan atau sudah dikunjungi, ke bawah
- Kalau tak dapat ke bawah atau sudah dikunjungi, ke kiri
- Kalau tak dapat ke kiri atau sudah dikunjungi, kembali ke tepat 1 petak sebelumnya lalu jalankan dari bagian pertama
Tentukan petak unik ke berapa dari urutan pengunjungan, Y dikunjungi oleh robot tersebut (anggap petak X merupakan petak pertama yang dikunjungi).
Deskripsi untuk soal nomor 10 - 11
Pak Dengklek membeli sekilo permen di pasar. Karena penasaran, ia ingin mengetahui berapa banyaknya sekilo permen yang dibelinya. Di pasar tersebut terdapat mesin penghitung permen yang ajaib, mesin ini dapat mengenali jumlah permen ganjil atau genap. Jika mesin tersebut dimasuki permen dengan jumlah genap, maka lampu indikator akan berwarna hijau, sedangkan jika ganjil akan berwarna merah, jika tidak ada permen di dalamnya maka lampu indikator akan mati. Pak Dengklek yang penasaran akhirnya memasukkan satu kilo permennya ke dalam mesin tersebut, kemudian mengamati nyalanya lampu indikator, jika berwarna hijau ia akan mengambil setengah dari permen yang ada di mesin tersebut. Lalu ia mengamati apa yang terjadi. Jika indikator menyala merah, maka ia akan mengambil satu permen dari mesin tersebut, memisahkannya ke dalam sebuah kantong, kemudian ia mengambil setengah dari yang tersisa di mesin ke dalam tasnya. Proses perhitungan menggunakan mesin dilakukan berulang hingga seluruh permen masuk ke tas atau masuk ke kantong Pak Dengklek dan indikator mesin mati.
Jika dalam penghitungan tersebut nyala lampu indikatornya adalah:
merah, merah, rnerah, hijau, rnerah, hijau, rnerah, merah, mati.
Berapakah jumlah sekilo permen yang dibeli Pak Dengklek seluruhnya?
Jika Pak Dengkek membeli 215 buah permen, berapakah jumlah permen yang tersisa di kantong saat melakukan penghitungan?
Cici robot si kelinci pandai meloncat dan akan dipakai Pak Dengklek untuk memanen tanaman. Pak Dengklek menanam 15 tanaman di halaman rumahnya dalam satu lajur dan jarak antara dua tanaman tidak harus sama. Diberikan data posisi 15 tanaman sebega! berikut:
2 9 17 31 59 72 94 103 141 152 179 211 241 288 293
Untuk mengambil 7 tanaman dalam 6 loncatan dari kiri ke kanan, tentukan loncatan terpendek yang maksimal.
Sebuah matriks berdimensi dua NxN akan diisi dengan bilangan, dengan pola penempatan bilangan secara tertentu. Beginilah pola tersebut pada matriks berukuran 5 x 5:
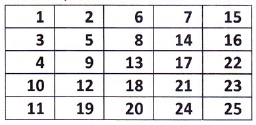
Apabila diketahui N = 4, berapakah nilai sel pada baris ke-2 dan kolom ke-3?
Sebuah matriks berdimensi dua NxN akan diisi dengan bilangan, dengan pola penempatan bilangan secara tertentu. Beginilah pola tersebut pada matriks berukuran 5 x 5:

Deskripsi untuk soal nomor 15 - 16
Terdapat suatu permainan dengan spesifikasi sebagai berikut:
1. Permainan tersebut terdiri dari sejumlah kartu, dimana kartu tersebut berada pada garis lurus dan setiap kartu terdiri dari sebuah angka.
2. Pak Dengklek akan menukar sebuah kartu dengan kartu yang persis di sebelahnya sesuai aturan tukar kartu yang akan diberikan.
3. Jika tak ada lagi kartu yang memenuhi aturan yang diberikan, maka permainan berakhir.
Jika diberikan bahwa terdapat 6 kartu, dengan urutan nilai pada kartu adalah 8, 5, -2, -1, 0, 0 dan aturan tukar kartu adalah angka pada kartu sebelah kanan lebih kecil dari kartu sebelah kiri, maka berapa kalikah Pak Dengklek akan melakukan pertukaran sampai permainan berakhir?
Jika diberikan bahwa terdapat 15 kartu, dengan urutan nilai pada kartu adalah 0, 3, 6, 9, 2017, 10, 11, 12, 13, 15, 14, 14, 15, 16, 17 dan aturan tukar kartu adalah angka pada kartu sebelah kanan lebih besar dari kartu sebelah kiri, maka berapa kalikah Pak Dengklek akan melakukan pertukaran sampai permainan berakhir?
Deskripsi untuk soal nomor 17 - 18
Pak Dengklek ingin mengambil harta karun di sebuah gua rahasia. Dalam gua tersebut ada 10 pundi-pundi yang diberi nomor 1 sampai dengan 10. Nomor urut dan isi setiap pundi-pundi adalah sebagai berikut:

Pak Dengklek mulai mengambil pundi-pundi ke-1 dan hanya boleh mengambll pundi-pundi dengan aturan sebagai berikut:
a. Jika ia memilih pundi-pundi yang berikutnya, setelah itu ia harus mengambil pundi-pundi dengan dua nomor urut berikutnya.
b. Jika ia mengambil pundl-pundi dengan dua nomor urut berikutnya, la dapat mengambil pundi-pundi berikutnya atau 2 nomor urut berikutnya
Berapakah jumlah berlian maksimum yang bisa diperoleh pak Dengklek setelah pundi-pundi bernomor urut terbesar diambiI?
Pada soal ini ada 16 pundi-pundi seperti tabel di bawah
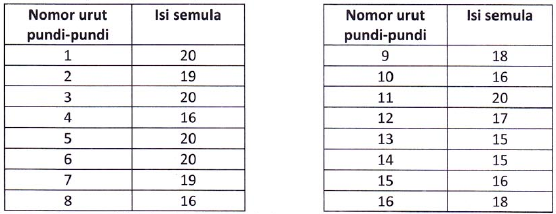
Pada kali ini, Pak Dengklek boleh mengubah urutan pundi-pundi sebelum melakukan pengambilan agar diperoleh total pengambilan maksimum. Tentukan berapa jumlah berlian maksimal yang diperoleh Pak Dengklek untuk sebuah gua dengan 16 pundi-pundi dengan pengurutan yang dapat ia lakukan, dan dengan aturan mengambil sama seperti pada deskripsi soal.
Pak Dengklek ingin memasak telur dadar menggunakan mesin-mesin pemecah, pengocok dan penggoreng yang bekerjanya tidak tergantung satu sama lain. Ada 3 tahapan untuk membuat telur dadar yaitu mulai memecah, kemudian mengocok, dan terakhlr menggoreng. Pak Dengklek memiliki 3 mesin pemecah telur, 2 mesin pengocok telur, dan 4 mesin penggoreng telur. Untuk bekerja, satu mesin pemecah butuh 3 menit/telur, satu mesin pengocok butuh 2 menit/telur, dan satu mesin penggoreng butuh 5 menit/telur. Waktu memindahkan telur dari satu mesin ke mesin lainnya dianggap tidak ada.
Contoh: Untuk memasak 3 telur waktu yang dibutuhkan adalah 12 men it dengan ilustrasi sebagai berikut:
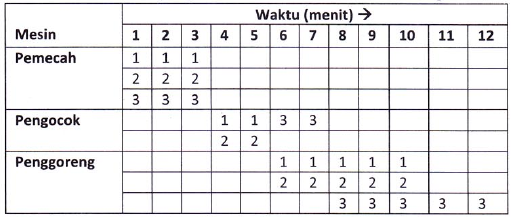
Berapa menitkah waktu minimum yang diperlukan untuk memasak 15 telur?
Di suatu hutan, terdapat seekor singa dan seekor harimau yang sedang berlomba untuk menentukan siapa yang pantas untuk menjadi raja hutan. Salah satu perlombaan yang dilombakan adalah melompat cepat untuk mengambil daging domba pada posisi tepat 100 meter dari posisi asal. Singa dan harimau harus melompat sepanjang sebuah garis lurus dan mulai pada posisi 1. Si singa tidak terlalu lincah dan hanya dapat melompat 2 kali tiap detik, sedangkan harimau dapat melompat 3 kali tiap detik. Tetapi singa lebih kuat dari harimau, sehingga jarak setiap lompatan singa mencapai 3 meter dibanding harimau yang hanya 2 meter tiap lompatan. Berdasarkan kemampuan meloncat tersebut, yang akan memenangkan perlombaan ini adalah ...
A, B, dan C bekerja untuk sebuah proyek dengan deadline 100 hari.
Jika A dan B saja yang bekerja, maka proyek selesai dalam 144 hari.
Jika A dan C saja yang bekerja, maka proyek akan selesal dalam 135 hari.
Jika B dan C saja yang bekerja, maka proyek akan selesai dalam 120 hari.
Agar proyek cepat selesai, mereka bertiga bekerja bersama-sama. Namun setelah 11 hari bekerja, A mendadak tidak datang. Pada hari keberapakah si A paling lambat harus datang kembali sehingga pekerjaan tersebut dapat selesai dengan tidak melebihi deadline?
Deskripsi untuk soal nomor 22 - 23
Ada 3 nada dering yang sedang terkenal di antara 40 siswa suatu kelas, yaitu om telolet om, tan telolet tan, dan bi telolet bi. Perbandingan banyak penggemar nada dering om telolet om dengan penggemar bi telolet bi adalah 2:3. Diketahui pula jumlah yang menggemari om telolet om sekaligus menggemari tan telolet tan dibandingkan dengan jumlah yang menggemari tan telolet tan sekaligus menggemari bi telolet bi adalah 1:2. Penggemar sejati suatu nada dering adalah penggemar yang hanya menyukai tepat 1 nada dering. Setelah dilakukan survei, ternyata penggemar om telolet om tidak menyukai nada dering bi telolet bi dan juga sebaliknya. Dan, banyaknya penggemar sejati bi telolet bi sama dengan banyaknya penggemar sejati om telolet om. Sementara, penggemar sejati tan telolet tan ada 20.
Hitunglah berapa selisih banyaknya penggemar bi telolet bi dengan banyaknya penggemar om telolet om!
Jika diketahui ada sejumlah siswa pindah kelas dan mereka bukan penggemar tan telolet tan, perbandingan penggemar om telolet om dengan penggemar bi telolet bi sekarang menjadi 3:4, maka tentukan berapa jumlah total penggemar maksimal om telolet om, tan telolet tan, dan bi telolet bi sekarang?
Deskripsi untuk soal nomor 24 - 25
Untuk p, q dan r yang berupa variabel boolean dan diberikan daftar simbol operator sebagai berikut:

Selanjutnya diberikan 2 pernyataan logika sebagai berikut:
p <=> (((q ^ (p v q)) -> ((q xor r) <=> (q v ~r))) v p)
q <=> ((q ^ (r v q)) -> ((p xor q xor r) -> (q ^ (q v ~q))))
Ada berapa kombinasi (p, q, r) sehingga kedua pernyataan logika di atas benar?
Jika s <=> ((p -> (q -> (r -> s))) -> (s -> (r -> (q -> p))))),
maka ada berapakah kombinasi (p,q,r,s) sehingga ketiga pernyataan logika tersebut terpenuhi?
A sedang berada di kutub utara planet P yang berbentuk bola sempurna, dengan jari-jari 5000 km. Dia melakukan perjalanan seperti berikut:
- 500 km ke Selatan
- 300 km ke Timur
- 400 km ke Selatan
- 100 km ke Barat
- 100 km ke Utara
Berapa jauh A dari titik semula?
Terdapat 12 buah paku yang tertancap pada sebuah papan. Sebuah karet gelang elastis akan dipasang mengelilingi sekumpulan paku seperti pada gambar di sebelah kanan. Paku-paku manakah yang akan disentuh karet gelang tersebut?
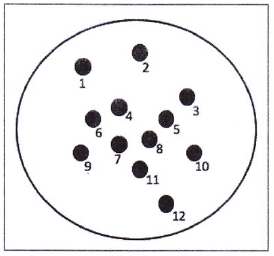
Diketahui empat premis (asumsi) sebagai berikut:
P ^ ~Q -> R ^ S
K -> G
~P -> K
L -> -Q
Tentukan nilai dari G dan L agar R bisa dipastikan benar!
Terdapat 4 orang yang sedang berbicara satu sama lain sebagai berikut. Diketahui beberapa orang berbohong dan yang lainnya berkata jujur.
A: Terdapat maksimal 1 orang yang berbohong.
B: Terdapat minimal 2 orang yang berbohong.
C: Terdapat maksimal 3 orang yang berbohong.
D: Terdapat minimal 4 orang yang berbohong.
Siapa sajakah orang-orang yang berbohong?
Anab lngln mengunjungi Jauhar. la harus melalui jalan-jalan searah yang dipenuhi monster. Anab memerlukan energi untuk melawan monster-monster tersebut. Anab akan kehilangan energi sebesar N untuk mengalahkan N monster. Setiap persimpangan jalan dijaga oleh Kingkong berkekuatan X sehingga Anab memerlukan energi minimal sebesar X untuk mengalahkan KingKong (jika energinya habis maka Anab akan mati). Anab ingin agar saat berjumpa dengan Jauhar, tenaganya masih tersisa sebesar mungkin. Peta jalan yang harus ditempuh Anas
dinyatakan dalam gambar berikut:
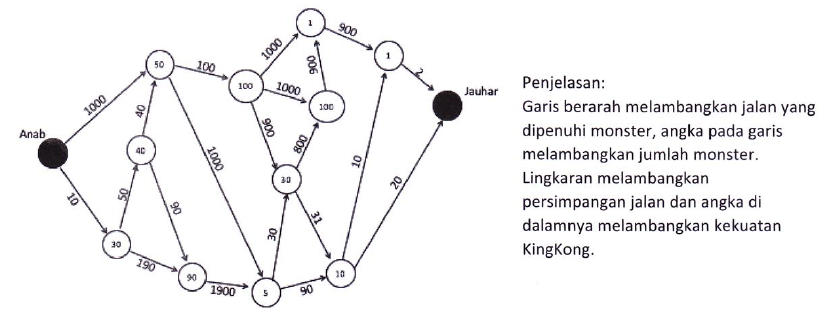
Jika tenaga awal Anab adalah 3000, berapakah tenaga maksimal yang masih dapat dimiliki Anab ketika sampai di tempat Jauhar?
Pak Dengklek adalah seorang kepala sekolah. Untuk meningkatkan mutu pendidikan di Indonesia, Pak Dengklek hendak mengirimkan stswanya untuk mengikuti olimpiade sains yang terdiri dari bidang: Matematika, Fisika, Kimia, Biologi, Astronomi, Kebumian, Geografi, Komputer, dan Ekonomi. Supaya sekolah dapat memilih siswa terbaik di bidangnya, setiap sekolah hanya boleh mengirimkan satu siswa untuk setiap bidang. Calon peserta yang akan dikirim Pak Dengklek berjumlah X, dengan bidang-bidang yang dikuasai sebagai berikut:
Turfa : bidang Kimia, Astronomi, Komputer
Jauhar : bidang Biologi, Kebumian, Komputer
Anab : bidang Biologi, Kebumian
Fahrni : bidang Astronomi, Kebumian
Ayaz : bidang Biologi, Komputer
Jona : bidang Biologi, Kebumian, Komputer
Setiap siswa hanya akan diikutkan olimpiade yang sesuai bidang keahliannya. Pak Dengklek sadar bahwa ada kemungkinan bahwa ia tidak dapat mengirimkan satu murid untuk setiap bidang olimpiade. Meskipun begitu Pak Dengklek ingin agar muridnya yang maju ke olimpiade sebanyak mungkin. Berapakah banyaknya murid maksimal yang dapat maju ke olimpiade?
Diberikan beberapa premis sebagai berikut:
Jika Rivin makan, maka Rivin kenyang.
Jika Rivin mandi, maka Rivin tidak kenyang.
Jika Rivin tidak kenyang, maka Rivin akan cepat lapar.
Jika diketahui kondisi awal bahwa 'Rivin tidak cepat lapar', mana sajakah yang dapat dipastikan dari premis berikut ini (setiap premis diberi nomor)?
- Rivin makan
- Rivin tidak makan
- Rivin mandi
- Rivin tidak mandi
- Rivin kenyang
- Rivin tidak kenyang
Tuliskan semua jawaban yang mungkin, dipisahkan tanda koma, dari nomor premis yang paling kecil. Apabila tidak ada jawaban yang benar, tuliskan angka -1.
Pak Ganesh telah membuat Pak Dengklek kesal, tapi kemudian ia menyesal dan ingin berbuat sesuatu sehingga dapat menyenangkan hati Pak Dengklek kembali. Pak Ganesh tahu, hanya ada beberapa kondisi yang dapat membuat Pak Dengklek menjadi senang kembali, tetapi tidak mudah, yaitu dengan membuatkan Pak Dengklek roti panggang.
- Sebuah rot! akan matang secara optimal jika dan hanya jika roti tersebut dipanggang dalam waktu paling cepat 7 menit dan paling lama 8 menit.
- Pak Dengklek akan senang apabila roti tersebut matang.
- Pak Ganesh memiliki waktu luang untuk memanggang roti pada Pukul 13:00 - 14:00 (termasuk mengambilnya).
- Waktu untuk mengambil roti dan memberikan ke Pak Ganesh dianggap 0 satuan waktu.
Pada pukul berapakah Pak Ganesh paling lambat dapat memulai pemanggangan, agar Pak Dengklek dapat menebus kesalahannya dan menyenangkan Pak Dengklek kembali?
Deskripsi untuk soal nomor 34 - 35
Pada suatu ruangan, terdapat 8 orang, yaitu A, B, C, D, E, F, G, H. Mereka sedang duduk di sebuah meja yang berbentuk lingkaran sempurna. Terdapat beberapa fakta sebagai berikut:
- Jarak antara 2 orang ditentukan dengan panjang garis lurus antara 2 orang tersebut.
- Jarak antara setiap pasangan yang bersebelahan adalah sama.
- Orang yang terjauh dari H adalah F.
- Jarak antara D ke H sama dengan jarak antara D ke F.
- Jarak antara A ke B lebih jauh daripada A ke G.
- Jarak antara C ke E sama dengan jarak antara C ke A.
- G berada 3 kursi di sebelah kiri (berlawanan arah dengan jarum jam) dari F.
- C merupakan orang yang terjauh dari G.
Siapakah yang berada pada 3 posisi di sebelah kiri H?
Jika ada satu tambahan aturan sebagai berikut:
- G tidak berada di tepat sebelah kiri B
Tentukan penempatan kedelapan orang tersebut pada meja, dimulai dari A dan berakhir pada orang di sebelah kanan A (searah putaran jarum jam), dlpisahkan spasi. Contoh: apabila B berada tepat di sebelah kiri A dan H berada di sebelah kanan A, maka salah satu konfigurasi yang mungkin adalah: A,B,C,D,E,F,G,H
Deskripsi untuk soal nomor 36 - 38
Pak Dengklek menciptakan suatu alat musik untuk para bebek asuhannya. Alat musik itu sangat canggih karena walaupun hanya dua tombol saja (tombol A dan B), ia dapat menghasilkan sejumlah bunyi: tang, ting, tung, teng, dan tong. Bunyi yang akan keluar bergantung pada bunyi apa yang tepat sebelumnya dan tombol apa yang akan dltekan kecuali penekanan pertama seperti terlihat pada tabel di bawah:
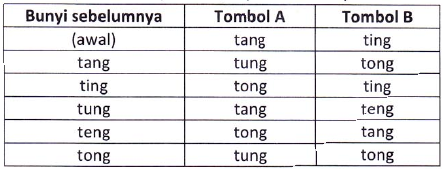
Sebenarnya, konfigurasinya bisa diatur sedemikian rupa dengan mengubah tabel di atas, sehingga penekanan tombol-tombol dapat menghasilkan deretan bunyi yang berbeda. Tapi kali ini, para bebek malah mengaturnya seperti tabel di atas. Para bebek mendefinisikan suatu permainan musik yang benar adalah jika bunyi terakhir tong.
Kwik mendapat giliran memainkan alat musik tersebut, la sudah merencanakan akan melakukan sejumlah penekanan tombol: ABAAABBAAABA. Karena ia malu jika permainan musiknya dianggap tidak benar, maka ia meminta Anda untuk mendapatkan deretan suara yang akan terdengar untuk deretan penekanan tersebut.
Tuliskan deretan penekanan tombol yang dapat menghasilkan deretan suara ting, ting, tong, tung, teng, tang, tong, tung, tang, tong.
Jika tombol pertama yang ditekan adalah A, bunyi apakah yang tidak akan pernah muncul pada setiap penekanan tombol apapun berikutnya?
Sejumlah batuan mengandung materi-materi (dengan rumus-rumus rnolekul kimiawi tertentu) yang tidak terdapat di bumi, telah diangkut oleh Explorer dari planet Tokinus ke bumi untuk diteliti oleh Profesor Dengklos. Setelah melalui sejumlah penelitian, Profesor Dengklos menemukan adanya materi-materi asing A, B, C, D, dan E dari batu-batuan itu. la juga menemukan sifat-sifat kimiawinya yang dinyatakan sebagai stoikiometri reaksi-reaksi berikut (catatan X, Y adalah materi yang melimpah terdapat di udara bumi):
2A + 3B -> 4C + 3E (1) X + 2C + 5D -> 3B (2) 5E + 1B -> 2D + 3A + 3Y (3)
Diketahui juga urutan tersebut menunjukkan prioritas, yaitu, jika dua reaksi bisa terjadi untuk materi yang sama, maka reaksi yang lebih atas yang akan dipilih terlebih dulu, kemudian materi sisanya untuk reaksi di bawahnya. Selain itu, setiap reaksi pasti berlangsung dalam satu unit waktu sedangkan satu unit terkecil (tidak dapat dipecahkan lagi) dari setiap materi adalah satu Tok. Sebagai contoh, pada reaksi (1), 2 Tok A dan 3 Tok B menghasilkan 4 Tok C dan 3 Tok B. Profesor Dengklos telah menguraikan sejumlah batu menjadi materi-materinya dalam kuantitas sebagai berikut (masing-masing dalam satuan Tok): A = 30, B = 20, C = 15, D = 25, dan E = 30. Berapa Tok materi Y yang dihasilkan pada waktu t = 5 ketika seluruh kuantitas itu dicampurkan kembali pada waktu t = 0?
Sebanyak 15 pramuka berbaris dalam satu sap. Masing-masing memegang sebuah bendera membentuk konfigurasi bendera. Mereka akan memainkan satu penampilan permainan konfigurasi bendera dengan mengangkat dan menurunkannya per detik mengikuti aturan sebagai berikut:
- Pramuka pada posisi ke k, 2 <= k <= 14,
- jika dalam keadaan mengangkat bendera, dan di kiri-kanannya ada yang menurunkan bendera, maka pada detik berikutnya ia akan menurunkan benderanya.
- jika dalam keadaan menurunkan bendera, jika di kiri-kanannya ada yang mengangkat bendera, maka maka pada detik berikutnya ia akan menaikkan benderanya.
- Selain itu, benderanya pada detik berikutnya tetap tidak berubah.
- Untuk pramuka pada posisi 1 dan 15 (ujung-ujung barisan), bila pada suatu detik ia melihat sebelahnya menurunkan bendera, pada detik berlkutnya ia akan menaikkan bendera, dan sebaliknya.
Kita lambangkan bendera terangkat dengan 1 dan bendera turun dengan 0, maka jika konfigurasi awal (detik ke 0) adalah 100101110011001, pada detik berikutnya menjadi 111010101100111. Dari konfigurasi awal 100101110011001 itu, bagaimanakah konfigurasi pada detik ke 5?
Diberikan fungsi seperti di bawah ini. Berapakah nilai yang dikembalikan dari pemanggilan fungsi cariNilai(2017,1017)?
function cariNilai(n, x: integer): longint;
var
i: integer;
n_now, x_now: integer;
ans: longint;
begin
ans := 0;
n_now := n;
x_now := x;
while (n_now > 0) do begin
ans := ans + x_now;
x_now := x_now - 1;
n_now := n_now - 1;
end;
cariNilai := ans;
end;
Diberikan fungsi seperti di bawah ini. Berapakah nilai dari f(8, 9, 4, 5, 6, 10000)?
function f (a, b , pa, pb, pab, n: longint): longint;
var
total: long int;
i: long int;
begin
i := 0;
total := 0;
while (total < n) do
begin
i := i + 1;
if (i mod a = 0) and (i mod b = 0) then
total := total + pab
else if i mod a = 0 then
total := total + pa
else if i mod b = 0 then
total := total + pb;
end;
f := i;
end;
Dlberikan potongan program seperti di bawah ini. Apa output dari potongan program tersebut, jika nilai dari haha = 9230 dan hehe = 4686?
while(true) do begin if (hehe = 0) then break; haha := haha mod hehe; if (haha = 0) then break; hehe : = hehe mod haha; end; writeln(haha + hehe);
Diberikan program di bawah ini. Apa output dari program tersebut apabila diberikan input (secara berurutan) yaitu 1000 dan 2
function apaini(x : integer) : integer;
var
ans, i : integer;
begin
ans := 0;
i := 1;
while (i <= x) do begin
if (x mod i = 0) then ans := ans + 1;
i := i + 1;
end;
apaini := ans;
end;
var
i : integer;
N : integer;
x : integer;
ans : integer;
begin
readln(N, x);
ans := 0;
for i := 1 to N do begin
if (apaini(i) mod x = 0) then
ans := ans + 1;
end;
writeln(ans);
end.
Tuliskan output program berikut.
program Soal1;
function ini(x: integer): integer; forward;
function soal(x: integer): integer; forward;
function gampang(x: integer): integer; forward;
function banget(x: integer): integer; forward;
function ini(x: integer): integer;
begin
if (x = 1) then
ini := 1
else
if (x <= 0) then
ini := 0
else
ini := -soal(x) + gampang(x);
end;
function soal(x: integer): integer;
begin
if (x <= 2) then
soal := -ini(x-1)
else
soal := -gampang(x) + banget(x) div 2;
end;
function gampang(x: integer): integer;
begin
if (x <= 3) then
gampang := ini(x-2)
else
gampang := -banget(x) div 2 + ini(x-4);
end;
function banget(x: integer): integer;
begin
if (x <= 4) then
banget := -2*ini(x-3)
else
banget := -2*(gampang(x-2) - soal(x-4));
end;
var
kenapa: integer;
begin
kenapa := ini(2) - soal(6) - gampang(5) + banget(4);
writeln(kenapa);
end.
GRID BERPOLA
Diberikan grid berukuran N baris dan M kolom. Dari baris teratas hingga terbawah dinomori dengan baris 1 hingga baris N, dan dari kolom terkiri hingga terkanan dinomori dengan kolom 1 hingga kolom M. Setiap petak pada grid diberi nomor dengan aturan pola berikut. Dimulai dari lapisan terluar grid diberi nomor 1, lapisan berikutnya yang lebih dalam diberi nomor 2, lapisan berikutnya diberi nomor 3, dan seterusnya. Berikut adalah contoh grid berukuran 7 baris dan 8 kolom yang telah diberi nomor.
Diberikan nilai N, M, X, dan Y. Anda diminta untuk membuat sebuah program yang menentukan nomor berapa yang ada di baris ke-X dan kolom ke-Y dari grid berukuran N baris dan M kolom.
Batasan :
1 N, M
10^9
1 X
N
1 Y
M
Format Input :
Sebuah baris yang berisi 4 bilangan bulat bertururt-turut yakni N, M, X, dan Y.
Format Output :
Sebuah baris yang berisi sebuah bilangan bulat yang menandakan nomor berapa yang ada di baris ke-X dan kolom ke-Y dari grid berukuran N baris dan M kolom.
Sample input dan output :
| 7 8 1 1 | 1 |
| 7 8 3 6 | 3 |
| 7 8 6 5 | 2 |
| 7 8 4 5 | 4 |
| 7 8 7 8 | 1 |
| 999 999 500 500 | 500 |
HUBUNGAN KAKEK-CUCU
Pada soal ini, Anda diminta untuk memroses silsilah dinasti kerajaan KITOKI. Setiap lelaki dinasti ini diberi nomor 1, 2, ... , N. Pendiri dinasti kerajaan diberi nomor 1. Anda diberi dafter hubungan ayah-anak, dimana A[Y]=X menyatakan bahwa Y adalah ayah dari X. Dari hubungan ayah-anak, Anda dapat mendeteksi hubungan kakek-cucu karena jlka z adalah ayah dari Y, dan Y adalah ayah dari X, maka Z adalah kakek dari X. Dari sebuah daftar hubungan ayah-anak, Anda diminta untuk membuat sebuah program yang menghitung banyaknya hubungan kakek-cucu.
Format Input :
Masukan terdiri dari 2 baris. Baris pertama berisi bilangan bulat N. Baris kedua berisi N-1 bilangan bulat A[2], A[3], hingga A[N] sesuai penjelasan pada deskripsi soal.
Format Output :
Sebuah baris yang berisi sebuah bilangan bulat yang menandakan banyaknya hubungan kakek-cucu dari data masukan yang diberikan.
Batasan :
1 N
100.000
1 A[i]
N
Dijamin bahwa daftar hubungan ayah-anak membentuk silsilah yang valid
Sample input dan output:
|
9 1 1 3 3 3 4 6 6 |
6 |
Penjelasan:
Berikut adalah tree yang dibentuk dari masukan di atas.
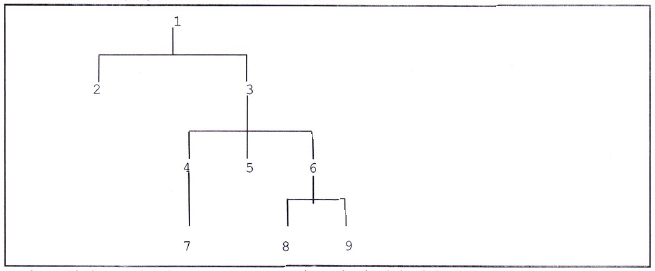
Terdapat 6 hubungan kakek-cucu pada tree tersebut yakni (1-4), (1-5), (1-6), (3-7), (3-8), dan (3-9).