Olimpiade Sains Kota (OSK) 2017 - Komputer
Berapakah banyaknya bilangan antara 1-1000, inklusif, dimana perkalian digit-digitnya merupakan
bilangan positif kelipatan 10?
a. 157
b. 156
c. 155
d. 154
e. 153
Jika diketahui A, B, C dan D adalah bilangan bulat dan memenuhi:
A.B + C + D = 3
B.C + A + D = 5
C.D + A + B = 2
D.A + B + C = 6
Berapakah nilai A yang dimaksud?
a. 0
b. 1
c. 2
d. 3
e. 5
Terdapat sebuah daftar yang memuat 2017 pernyataan sebagai berikut:
Pernyataan nomor 1: “Terdapat tepat 1 pernyataan dalam daftar ini yang salah.”
Pernyataan nomor 2: “Terdapat tepat 2 pernyataan dalam daftar ini yang salah.”
Pernyataan nomor 3: Terdapat tepat 3 pernyataan dalam daftar ini yang salah.”
...
Pernyataan nomor 2017: “Terdapat tepat 2017 pernyataan dalam daftar ini yang salah. “
Pernyataan nomor berapakah yang benar jika ternyata hanya ada satu yang benar?
a. 2004
b. 2008
c. 2016
d. 2017
e. Jawaban a, b, c, d salah
Berapa banyak cara berbeda untuk mengisi lantai sebuah ruangan berukuran 2x8 dengan menggunakan ubin berukuran 2x1, jika harus terdapat tepat 2 ubin yang dipasang secara vertical?
a. 7
b. 8
c. 9
d. 10
e. 11
Sebuah brankas dilengkapi dengan kunci kombinasi 4 dijit. Masing-masing dijit memiliki 2 kemungkinan nilai, yaitu 0 dan 1. Ternyata, diketahui diantara 4 dijit itu, hanya 2 dijit yang berfungsi untuk mengunci brankas tersebut. Berapakah banyak percobaan minimal untuk dapat membuka brankas tersebut?
a. 3
b. 6
c. 12
d. 18
e. 24
Adi dan Budi adalah murid dari sebuah kelas yang terdiri dari 40 siswa. Dari kelas tersebut akan dipilih 20 orang siswa sebagai wakil kelas. Wakil kelas dipilih dengan cara membagi 40 orang siswa menjadi 20 grup. Tiap grup melempar sebuah koin untuk menentukan siapa yang akan mewakili kelas tersebut. Jika peluang Adi dan Budi terpilih untuk mewakili kelas tersebut adalah , dimana
dan
saling prima, berapakah
+
?
a. 91
b. 93
c. 95
d. 97
e. 99
Berapakah mod
?
a. 0
b. 2
c. 4
d. 6
e. 8
Terdapat 6 buah pekerjaan, A, B, C, D, E, dan F. Pekerjaan ini harus dikerjakan dengan mengikuti aturan sebagai berikut:
- Pekerjaan F harus dikerjakan sebelum pekerjaan A
- Pekerjaan B harus dikerjakan sebelum pekerjaan D
- Pekerjaan E dapat dikerjakan jika pekerjaan B sudah dikerjakan
- Sebelum mengerjakan pekerjaan B, pekerjaan C harus sudah dilakukan
- Pekerjaan A harus dikerjakan sebelum pekerjaan B
Salah satu urutan pengerjaan pekerjaan yang dapat dilakukan adalah…
a. D, B, F, C, A, E
b. C, F, A, D, B, E
c. C, B, F, A, E, D
d. F, C, A, D, B, E
e. F, A, C, B, E, D
String biner adalah deretan karakter yang setiap karakternya adalah ‘0’ atau ‘1’. Substring dari suatu string adalah potongan dari string itu atau string itu sendiri. Berapa banyak string biner dengan panjang 9 yang tidak berisi substring ‘100’?
a. 113
b. 143
c. 168
d. 232
e. 253
Pak Adi adalah seorang guru. Ia mengajar 3 kelas, masing-masing berisi 7, 11, dan 13 siswa. Suatu saat, Pak Adi ingin membeli dan membagikan sejumlah permen kepada semua siswa pada salah satu kelas. Jika permen dibagikan ke kelas pertama (7 siswa), maka ada 1 anak yang akan mendapatkan lebih banyak dari yang lain. Jika dibagikan ke kelas kedua (11 siswa), akan ada 8 anak yang mendapat lebih banyak dari yang lain. Jika dibagikan ke kelas ketiga (13 siswa), akan ada 6 anak yang akan mendapat lebih banyak dari yang lain. Berapa jumlah minimal permen agar jika dibagikan ke satu kelas manapun semua siswa akan mendapatnya dalam jumlah yang sama?
a. 331
b. 543
c. 741
d. 839
e. 1001
Pak Dengklek mempunyai N buah kartu yang telah diberi nomor 1, 2, 3,..., N. Pada awalnya, Pak Dengklek menyusun kartu-kartu tersebut secara ascending (menaik). Selanjutnya, Pak Dengklek ingin menyusun kartu-kartu tersebut dengan aturan tidak boleh ada satu kartupun yang berada pada posisi yang sama dengan posisi awalnya. Jika N=7, berapa banyak susunan yang sesuai dengan aturan di atas yang dapat dibentuk oleh Pak Dengklek?
a. 49
b. 5040
c. 1854
d. 5481
e. 4815
Berapa banyak kata sepanjang N-karakter yang dapat dibentuk dari angka-angka {0, 1, 2}, sedemikian sehingga angka-angka yang saling bersebelahan hanya berselisih maksimum 1. Contoh : Untuk N=2 terdapat 7 kata yang dapat dibentuk yaitu : <0 0>, <0 1>, <1 0>, <1 1>, <1 2>, <2 1>, <2 2>. Notasi < > menyatakan bentukan satu kata. Jika N=10, berapa banyak kata yang dapat dibentuk?
a. 8119
b. 8121
c. 8123
d. 8125
e. 8127
Di sebuah meja melingkar untuk 100 orang, 4 orang akan melakukan jabat tangan satu sama lain. Berapa banyak cara memilih 4 orang tersebut sedemikian sehingga tidak ada orang bersebelahan yang berjabat tangan?
a. 3460375
b. 3921225
c. 3764376
d. 3321960
e. 3640753
Pelatih olah raga meminta 3 atlet binaannya bernama Dengklek, Ganesh, Blangkon untuk berlari mengelilingi lapangan olah raga dengan target sebanyak 5 keliling. Kondisi yang diperoleh adalah:
- Jika Blangkon tidak menyelesaikannya paling awal, maka Dengklek yang menyelesaikan paling awal dari ketiganya.
- Jika Dengklek tidak menyelesaikannya paling akhir, maka Ganesh yang menyelesaikan paling awal dari ketiganya.
Dari sejumlah kondisi di atas, bagaimana urutan pencapaian target mulai dari yang paling awal menyelesaikan tagetnya?
a. Dengklek, Ganesh, Blangkon
b. Ganesh, Dengklek, Blangkon
c. Blangkon, Ganesh, Dengklek
d. Blangkon, Dengklek, Ganesh
e. Dengklek, Blangkon, Ganesh
Deskripsi untuk soal nomor 15 - 17
Sekolah di negeri TOKI terdiri atas jurusan MIA dan jurusan IIS. Masing-masing jurusan mengajarkan sejumlah mata pelajaran. Ada sejumlah pelajaran yang diberikan di kedua jurusan tersebut. Dengklek belajar di jurusan MIA dan Ganesh di jurusan IIS. Dengklek dan Ganesh mengikuti sejumlah pelajaran yang sama. Untuk memudahkan, kelompok pelajaran tersebut mereka namakan IBB. Setiap pelajaran di jurusan MIA atau di jurusan IIS, dikelompokkan pada kelompok yang mereka namai SMA, dimana tidak ada 2 atau lebih pelajaran yang sama di kelompok SMA.
Apabila pelajaran di IIS adalah “Ekonomi”, “Geografi”, dan “Bahasa Indonesia”; sedangkan pelajaran di MIA adalah “Fisika”, “Bahasa Indonesia”, “Kimia”, dan “Biologi”; pelajaran apa saja yang ada di IBB dan SMA?
a. “Bahasa Indonesia”
b. “Fisika”
c. “Geografi”
d. “Kimia”
e. Tidak ada pelajaran yang memenuhi
Apabila dibuat kelompok baru bernama NEW yang terdiri dari pelajaran-pelajaran yang ada di kelompok IBB atau kelompok SMA, berapakah jumlah pelajaran yang ada di kelompok NEW?
a. Sama dengan jumlah pelajaran di kelompok IBB
b. Sama dengan jumlah pelajaran di kelompok SMA
c. Sama dengan jumlah pelajaran MIA ditambah dengan jumlah pelajaran IIS
d. Sama dengan selisih jumlah pelajaran MIA dengan jumlah pelajaran IIS
e. Nol
Apabila dibuat kelompok baru bernama EXT yang berisi pelajaran MIA namun bukan pelajaran IIS, maka pelajaran-pelajaran yang merupakan gabungan dari kelompok EXT dan kelompok IBB adalah …
a. Pelajaran-pelajaran di SMA
b. Pelajaran-pelajaran di IBB
c. Pelajaran-pelajaran di IIS
d. Pelajaran-pelajaran di MIA
e. Jawaban a, b, c, dan d salah
Bilangan bulat non negatif 0, 1, 2, … diletakkan pada koordinat (x,y) seperti pada gambar sebelah kanan. Sebagai contoh, bilangan 0, 1, dan 2 diletakkan pada koordinat (0,0), (1,1), dan (2,0). Berapa koordinat untuk bilangan 2017?
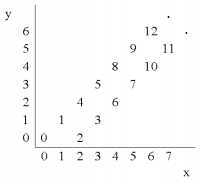
a. (1008,1009)
b. (1008,1008)
c. (1009,1001)
d. (1009,1008)
e. (1009,1009)
Setiap akhir hari Jumat, enam orang mata-mata (M1, M2, M3, M4, M5, M6) saling menukar informasi yang berhasil mereka dapatkan selama seminggu kerja. Seorang mata-mata tak dibolehkan untuk bertemu dengan lebih dari satu mata-mata lainnya pada satu saat. Maka, mereka harus mengatur pertemuan agar dapat bertemu dalam beberapa kali, di mana pada setiap pertemuan dihadiri oleh sepasang mata-mata dan saat itu keduanya berbagi informasi yang mereka punyai saat itu. Sebelum pertemuan, setiap orang mata-mata hanya tahu satu informasi (M1 tahu 'a', M2 tahu 'b, M3 tahu ‘c’, M4 tahu ‘d’. M5 tahu ‘e’ dan M6 tahu ‘f’.).
Kelompok 6 mata-mata tersebut membutuhkan hanya 3 kali pertemuan untuk berbagi semua informasi seperti ditunjukkan pada rangkaian gambar sebagai berikut.
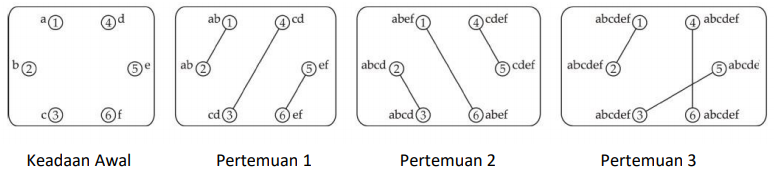
Jadi, dengan 3 kali pertemuan, setiap mata-mata mendapatkan semua informasi.
Karena suatu hal penting, salah satu mata-mata berhenti bekerja. Berapa kali pertemuan yang dibutuhkan agar lima mata-mata sisanya mendapatkan semua informasi ?
a. 2
b. 3
c. 4
d. 5
e. 6
Jika semua A adalah B dan sebagian B adalah C, manakah pernyataan di bawah ini yang benar?
a. Semua A adalah C
b. Sebagian C adalah A
c. Semua C adalah A
d. Sebagian A adalah C
e. Jawaban a, b, c, dan d salah
Dalam suatu kelas, terdapat 40 siswa. 19 siswa menyukai matematika, 10 siswa menyukai komputer, 5 siswa menyukai fisika, 2 siswa menyukai ketiganya, 3 siswa menyukai matematika dan fisika saja, dan 7 siswa menyukai matematika saja.
Berapa banyaknya siswa yang tidak menyukai apapun?
a. 28
b. 6
c. 20
d. 19
e. 15
Satu toko baju menjual sejumlah kemeja dalam 3 ukuran: S, M dan L, dan berwarna hijau atau biru.
Diketahui juga bahwa:
- Kemeja berukuran S dan berwarna hijau ada 7 lembar.
- Kemeja biru berukuran L ada 2 lembar.
- Kemeja berwarna biru ada 14 lembar.
- Kemeja yang tidak berukuran S ada 19 lembar.
- Separuh kemeja-kemeja itu berukuran M.
- Banyaknya kemeja berukuran L sama dengan yang berukuran S warna biru.
Berapa seluruh kemeja di toko itu?
a. 16
b. 21
c. 30
d. 33
e. 40
Sepasukan semut berjalan di suatu lintasan jalan semut. Dalam lintasan terdapat celah-celah sempit vertikal seukuran badan semut dengan kedalaman beberapa panjang semut. Untuk menyeberangi celah, semut-semut paling depan turun ke dalam dasar celah hingga celah tertutup badan-badan semut itu. Yang paling depan menempati yang paling bawah dalam celah. Kemudian semut-semut di belakangnya dapat menyeberangi celah dengan melalui semut-semut itu. Setelah mereka lewat, semut dalam celah mulai dari yang teratas naik ke permukaan bergabung kembali di belakang barisan dengan urutan yang teratas duluan. Contohnya, semula urutan: 1,2,3,4,5,6,7,8,9,10 (paling depan adalah terkiri, paling belakang adalah terkanan, bergerak dari kanan ke kiri), saat melalui celah kedalaman 4, urutan 1, 2, 3, 4 masuk ke dalam celah, sisanya 5,6,7,8,9,10 melewatinya. Setelah itu keempat bergabung dengan urutan terbalik di belakang sehingga sekarang urutannya 5,6,7,8,9,10,4,3,2,1.
Pada awalnya, ada 10 semut yang berbaris dalam urutan: 1,2,3,4,5,6,7,8,9,10. Setelah melalui 5 celah yang masing-masing dengan kedalaman 7, 6, 3, 5, dan 4, urutan setelah melalui celah terakhir adalah:
a. 4,10,7,6,5,1,3,2,8,9
b. 4,3,2,1,5,6,7,10,9,8
c. 8,9,10,7,6,5, 4,3,2,1
d. 1,5,6,7,10, 9,8,2,3,4
e. 9,8,2,3, 4,10,7,6,5,1
Deskripsi untuk soal nomor 24 - 25
Pak Totok adalah pedagang keliling. Setiap hari ia berjualan di suatu kampung dan besoknya berpindah ke kampung lain. Namun, ia memiliki aturan-aturan sbb. Pak Totok selalu berjualan di 4 kampung berbeda yaitu: A, B, C, dan D.
- Jika hari ini ia ada di A, maka besoknya akan pasti pindah ke C.
- Jika hari ini ia ada di B maka hari berikutnya ia akan berada di A atau D.
- Jika hari ini ia ada di C maka besoknya ia akan ke B atau D.
- Jika hari ini ia ada di D maka besoknya ia pasti akan berada di A.
Jika pada suatu hari ia ada di A, dimanakah ia bisa berada 3 hari kemudian?
a. A atau B
b. A atau C
c. B atau C
d. A atau D
e. B atau D
Jika pada suatu hari ia berada di A, 20 hari kemudian berada di suatu kampung X. Kampung apakah yang tidak mungkin sebagai X?
a. A
b. B
c. C
d. D
e. Jawaban a, b, c, dan d salah
Deskripsi untuk soal nomor 26 - 27
- Proses sebuah mesin terkait pada 5 macam materi: A, B, C, D dan E.
- Proses pertama mengolah setiap 3 unit A dan 2 unit B menghasilkan 3 unit D.
- Proses kedua mengolah setiap 1 unit A, 1 unit C, dan 1 unit D menjadi 2 unit E dan 3 unit B.
- Proses ketiga mengolah setiap 1 unit E dan 1 unit D menjadi 2 unit A.
Setiap proses segera terjadi jika setiap bahan yang diperlukan tersedia dan hasilnya diperoleh tepat 1 jam kemudian. Proses juga bisa terjadi secara paralel misalnya jika tersedia 6 unit A dan 4 unit B, maka satu jam berikutnya dua proses pertama akan menghasilkan 6 unit D.
Jika mula-mula terdapat 5 unit A, 3 unit B, dan 1 unit C, ada berapa banyak materi A tepat pada 3 jam berikutnya?
a. 1 unit
b. 2 unit
c. 3 unit
d. 4 unit
e. 5 unit
Jika semula terdapat 10 unit A, 4 unit C dan 6 unit D, ada berapa banyak materi D setelah tepat 4 jam berikutnya?
a. 6 unit
b. 8 unit
c. 10 unit
d. 12 unit
e. 14 unit
Deskripsi untuk soal nomor 28 - 29
Suatu robot bergerak di atas suatu rel yang terentang dari kiri ke kanan dengan ujung pada jarak yang cukup jauh. Pada rel tertera angka-angka posisi per10cm membesar ke kanan, mulai dari 0cm, 10cm, 20cm, … dst. Robot akan bergerak menuruti deretan instruksi yang diberikan. Robot dapat menuliskan/ menghapus tanda X pada posisi robot. Instruksi-instruksi didefinisikan sebagai berikut:
- [R] memerintahkan robot untuk berpindah 10 cm ke kanan,
- [L] memerintahkan robot untuk berpindah 10 cm ke kiri,
- [W] memerintahkan robot untuk menuliskan X pada posisinya,
- [H] memerintahkan robot untuk menghapus X pada posisinya (jika ada),
- [RX] memerintahkan robot untuk berpindah ke kanan sampai ketemu tanda X atau berhenti jika mencapai ujung kanan rel.
- [LX] memerintahkan robot untuk berpindah ke kiri sampai ketemu tanda X atau berhenti jika mencapai ujung kiri rel.
- Rep(n,…) adalah perintah untuk dapat melakukan pengulangan deretan perintah yang dituliskan menggantikan “….” sebanyak n kali, sementara
- Rep(…) adalah perintah pengulangan terus menerus yang akan berhenti karena [LX] atau [RX] mencapai ujung rel.
Pada suatu saat robot berada di posisi 0cm dan sejumlah tanda X diletakkan di posisi 80cm, 130cm dan 180cm. Pada robot diberikan perintah
[RX] [RX] [H] [LX] Rep(3, [L] ) [W] [RX] [RX] [H] [LX] [LX] (Rep(3, [L] ) [W]
Dimanakah posisi robot beserta tanda-tanda X itu sekarang?
a. 0cm, 50cm, dan 80cm
b. 20cm, 50cm dan 80cm
c. 20cm, 80cm, dan 130cm
d. 50cm, 130cm, dan 180cm
e. 100cm, 130cm, dan 180cm
Jika pada suatu saat robot berada di posisi 0cm, sejumlah tanda X berturut-turut berada pada suatu posisi di sebelah kanannya (lebih dari satu tanda X). Kemudian, robot menjalankan deretan perintah ini:
Rep(2, [RX] [H] ) [L] [W] [R] Rep(Rep(2, [RX] [H] ) [LX] [R] [W] )
Ada berapa banyak kah tanda X saat robot berhenti jika sebelumnya ada 11 tanda X?
a. 0
b. 5
c. 10
d. 15
e. 20
Limabelas pramuka berbaris dalam satu saf. Masing-masing memegang sebuah bendera membentuk konfigurasi bendera. Mereka akan mempertunjukkan satu permainan konfigurasi bendera dengan aturan bahwa setiap detik setiap pramuka akan mengangkat dan menurunkan benderanya sebagai berikut.
- Pramuka pada posisi ke k, 2 k
14,
- jika dalam keadaan mengangkat bendera, dan sekurangnya salah satu di kiri/kanannya dalam keadaan mengangkat bendera, maka pada detik berikutnya ia akan menurunkan benderanya.
- jika dalam keadaan menurunkan bendera, jika di kiri/kanannya ada yang tidak mengangkat bendera, maka maka pada detik berikutnya ia akan mengangkat benderanya.
- Selain itu, posisi benderanya pada detik berikutnya tetap.
- Untuk pramuka pada posisi 1 dan 15 (ujung-ujung barisan), ia akan menaikkan bendera jika sebelahnya turun atau sebaliknya sehingga pada detik berikutnya benderanya akan berada pada posisi bendera yang berlawanan dengan posisi bendera sebelahnya pada detik ini.
Kita lambangkan bendera terangkat dengan 1 dan bendera turun dengan 0, maka jika konfigurasi awal adalah 100101110011001, pada detik berikutnya menjadi 111100001100111. Dari konfigurasi awal (detik ke 0) adalah 100101110011001, bagaimanakah konfigurasi pada detik ke 5?
a. 111100001101111
b. 000011110011000
c. 111100001100111
d. 000011110011000
e. 111100001100111
Diberikan gambar sistem aliran gas beracun sebagai berikut :
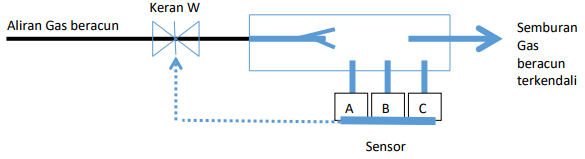
Pada sistem tersebut, semburan gas diatur dengan keran W yang dibuka atau ditutup berdasarkan sinyal dari sensor A, B dan C.
Pada sistem tersebut, semburan gas diatur dengan keran W yang dibuka atau ditutup berdasarkan sinyal dari sensor A, B dan C. Keran W akan dibuka jika Sensor A, B, dan C berfungsi dengan baik (memberikan signal TRUE). Untuk keselamatan, jika semua sensor A dan B dan C gagal berfungsi (memberikan signal FALSE), maka keran W harus ditutup. Selain itu, keran W hanya akan dibuka jika minimal dua dari ketiga sensor tersebut berfungsi dengan baik (memberikan signal TRUE).
Tuliskan ekspresi boolen untuk membuka keran yang mewakili pernyataan di atas, sebagai fungsi boolean kondisi A, B dan C
a. (A and (B or C)) or (B and (A or C))
b. A and B and C
c. (A or B) and (A or C) and (B or C)
d. (A and B) or (B and C)
e. (A or B) or B or C
Pada suatu pabrik, produk harus diproses melalui dua stasiun kerja, yaitu Stasiun-Persegi dan Stasiun-Bundar. Ada dua jenis produk yang harus diproses yaitu produk bintang (B) dan produk Smiley (S). Aturan produksi adalah sebagai berikut:
- Hanya ada satu produk dapat berada pada satu stasiun kerja.
- Setiap produk harus diproses dulu di Stasiun-Bundar, baru kemudian diproses di stasiun-Persegi
- Setelah diproses di sebuah stasiun, produk mungkin saja harus menunggu sebelum diproses ke stasiun berikutnya.
- Tepat setiap dua produk bintang harus diproses di Stasiun-Bundar kemudian diikuti tepat dua produk smiley (jadi bintang harus menunggu setelah satu smiley diproses), kecuali yang tersisa.
- Tepat setiap satu produk smilley harus diproses lebih dulu dari tepat dua produk bintang di stasiun persegi, kecuali yang tersisa.
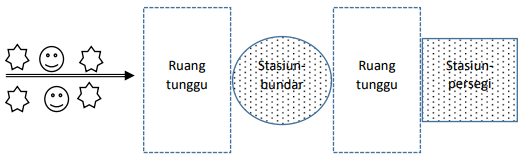
Jika awalnya ada 2 smiley dan 4 bintang, bagaimana urutan produk setelah keluar dari stasiun persegi (ditulis sebagai string dengan simbol-simbol B dan S, dan yang paling kiri adalah yang terakhir keluar)?
a. BSBBSB
b. BBSBBS
c. BBSSBB
d. SSBBBB
e. SBBSBB
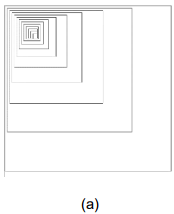
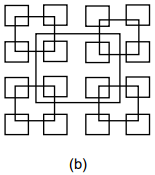
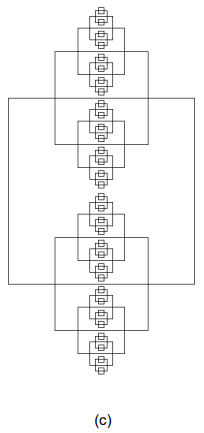
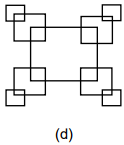
Sebuah prosedur rekursif adalah program yang memanggil prosedur tersebut.
Berikut ini adalah contoh dari prosedur rekursif.
Sebuah Prosedur DrawSquare(x,y,s) memberi instruksi ke komputer agar melakukan langkah sebagai berikut:
- Gambar sebuah persegi bersisi s yang titik tengahnya adalah (x,y).
- Jika sisi persegi lebih besar dari 2 piksel:
- DrawSquare(x+s/2,y,s/2) (gambar sebuah persegi lebih kecil ke kanan)
- DrawSquare(x-s/2,y,s/2) (gambar sebuah persegi lebih kecil ke kiri)
Pola gambar mana yang dihasilkan oleh DrawSquare?
Pak Dengklek harus membawa itik-itiknya melewati terowongan dari stasiun S ke stasiun T. Pada gambar setiap stasiun digambarkan sebagai lingkaran. Itik-itik tersebut harus berjalan melalui terowongan dengan arah yang ditunjukkan pada gambar, dari satu stasiun ke stasiun lain. Setiap terowongan mempunyai kapasitas itik yang dapat lewat dalam sehari, yang jumlahnya dinyatakan dalam angka pada gambar. Dari sebuah stasiun, Pak Dengklek dapat mengirim itik-itiknya melalui terowongan yang tersedia pada stasiun tersebut ke stasiun berikutnya.
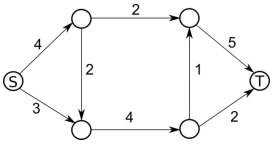
Berapa jumlah itik maksimum yang dapat dipindahkan oleh Pak Dengklek dari S ke T dalam satu hari?
a. 4
b. 5
c. 6
d. 7
e. 8
Deskripsi untuk soal nomor 35 - 36
Perhatikan potongan kode berikut:
var
n, temp : longint;
begin
readln(n);
while n >= 10 do
temp := 1;
while n > 0 do
begin
temp := temp * (n mod 10);
n := n div 10;
end;
n := temp;
end.
Berapakah nilai akhir n, jika nilai n pada awalnya adalah 62792912?
a. 4
b. 5
c. 6
d. 7
e. 8
Berapakah nilai akhir n, jika nilai n pada awalnya adalah 14934976?
a. 4
b. 5
c. 6
d. 7
e. 8
Perhatikan pseudocode berikut:
function f(x: integer) : integer; begin if(x = 0) then f := 0 else f := 1 - f(x - 1); end;
Ada berapa banyak nilai f(n) (1 <= n <= 2017) yang bernilai true?
a. 1008
b. 1009
c. 2016
d. 2017
e. 1
Perhatikan pseudocode berikut:
procedure mystery(a:integer; b:integer;);
var m:integer;
begin
if (a <> b)
begin
writeln(‘OSK2017’);
m := (a + b) / 2;
mystery(a, m);
mystery(m, b);
end;
end;
Berapa kali teks ‘OSK2017’ dicetak pada pemanggilan mystery(0,8) ?
a. 4
b. 5
c. 6
d. 7
e. program tidak pernah berhenti
Deskripsi untuk soal nomor 39 - 40
Perhatikan potongan kode berikut:
var
n, count : integer;
begin
readln(n);
count := 0;
repeat
n := (n * n + 5) mod 23;
count := count + 1;
until n = 0;
end.
Berapakah hasil akhir dari variabel count, jika n = 1?
a. 5
b. 6
c. 7
d. 8
e. 9
Berapakah nilai maksimal dari variabel count dari semua kemungkinan nilai n?
a. 6
b. 7
c. 8
d. 9
e. Jawaban a, b, c, d salah